Sunrise and Sunset Times Near the Solstices

The period within a few weeks of the winter solstice in late December is the darkest time of the year for northern latitudes. Not only does the Sun traverse its lowest arc across the sky at this time, but in many places the Sun sets before the end of a normal workday and rises after many people have already started their daily routines. At latitude 40° north, earliest sunset occurs around December 8 each year, and latest sunrise occurs around January 5. The day with the least amount of daylight is the winter solstice, the first day of winter, on or about December 21. Why are not all these dates the same? The answer is not trivial, but on this page we have tried to provide as simple an explanation as possible. It has to do with the fact that our clocks and the Sun do not keep the same kind of time. Below are three explanations, with increasing detail. Choose the one that most fits your level of interest!

By the way, a similar situation occurs at the summer solstice, for the same basic reason, though the effect is not as extreme. Solstice occurs around June 21, but at latitude 40° north the earliest sunrise occurs around June 14 and the latest sunset occurs around June 28. The changing times of sunrise and sunset are probably more noticeable in the winter months, because sunrise and sunset occur when we are more likely to be paying attention — when we're starting our day and during the evening rush hour. Also, most of us don't like the short period of daylight then and are looking forward to getting more of it.

Note: These explanations are written from a northern-hemisphere perspective. The situation is similar in the southern hemisphere.

A Thumbnail Explanation

Our clocks do not keep Sun time. Time measured by the position of the Sun in the sky is somewhat variable over the course of a year, but our clocks keep a uniform approximation to Sun time with each day exactly 24 hours long. One consequence of this is that sundials usually seem to be wrong; that is, they do not keep clock time. The times of sunrise and sunset, measured by the clock, are also affected by the difference between the two kinds of time. Although the length of daylight is shortest on the winter solstice, around December 21, the dates of earliest sunset and latest sunrise are, somewhat surprisingly, not on this date. Why is that?

The reason can be traced to the fact that the difference between Sun time and clock time is rapidly changing in December and January. The Sun runs slow compared to clock time then, so the times of both sunrise and sunset tend to be a bit late according to the clock, delayed from one day to the next by up to a half minute. Consequently, the time of sunset begins to shift later at an earlier date than we would expect (so that the earliest sunset is in early December), and the time of sunrise doesn't begin to shift earlier until a later date than we would expect (so that the latest sunrise is in early January).

Expanding a Bit . . .

The changing position of the Sun in the sky over the course of a day is mainly an effect of the Earth's rotation on its axis, which is quite uniform to a small fraction of a second. However, where the Sun appears in the sky at any given time is also affected by the position of the Earth in its orbit around the Sun. For reasons explained elsewhere, time kept by the Sun is not uniform throughout the year. Some solar days (the interval between the instants when the Sun is due south in the sky) are longer or shorter than 24 hours by as much as a half minute. On the other hand, our clocks keep civil time, with a uniform rate equal to the solar rate averaged over the entire year, with each day exactly 24 hours long. Therefore, even very carefully made sundials located in the middle of a time zone do not keep clock time.

Regardless of what kind of time we use, the day with the shortest overall length of daylight is always the winter solstice, on or about December 21, when the Sun appears to move along its most southern track in our sky. If we kept time by the Sun, and not mechanical or electrical clocks, the date of the earliest sunset and the date of the latest sunrise would also be the date of the winter solstice. This is what most people (even astronomers!) would expect: the solstice, earliest sunset, and latest sunrise should "naturally" occur on the same date.

But our clocks do not run on Sun time. In fact, actual solar days from mid November to early February are each longer than 24 hours by anywhere from a few seconds to a half minute. In other words, the Sun moves with what seems to be a very slightly slower-than-average apparent westward daily motion in the sky (measured with respect to our uniform clock time) during that part of the year. This tends to delay both sunrises and sunsets as measured by the clock. As a result, the times of sunset start moving later before the date of the solstice (that is, the date of earliest sunset occurs early) and the times of sunrises do not start moving earlier until after the date of the solstice (the date of latest sunrise occurs late). How much these two dates differ from that of the winter solstice depends on your latitude; at 40° north latitude, these dates are about two weeks from the solstice, earlier or later, respectively. The range of these dates is wider at lower latitudes and narrower at higher latitudes.

The Long Story

The Earth's seasons are caused by three factors:

The Earth orbits the Sun once a year in a nearly circular orbit.
The Earth's axis of rotation (the straight line through the center of the Earth between the north and south poles) is not perpendicular to the plane of the Earth's orbit. The Earth's axis is tilted by about 23.4° from the the direction perpendiular to the orbital plane.
The orientation of the Earth's axis in space remains nearly constant even as the Earth revolves around the Sun. It always points in the general direction of the star Polaris.

The result is that when the Earth is on one side of its orbit, the south pole is tilted toward the Sun (by as much as 23.4°) and the southern hemisphere experiences summer. Six months later, when the Earth is on the opposite side of its orbit, the north pole is tilted toward the Sun (by as much as 23.4°) and the northern hemisphere experiences summer. What we see from our viewpoint in the Earth's northern hemisphere is that the Sun's apparent daily track across the sky is much higher (that is, more northerly) in summer, and lower (more southerly) in winter. From horizon to horizon, the Sun's track is longer in summer and shorter in winter; so that in summer, sunrises are much earlier and sunsets are much later than in winter. See, for example, the graphic below, or this photograph of the Sun's paths through the sky at different times of the year.

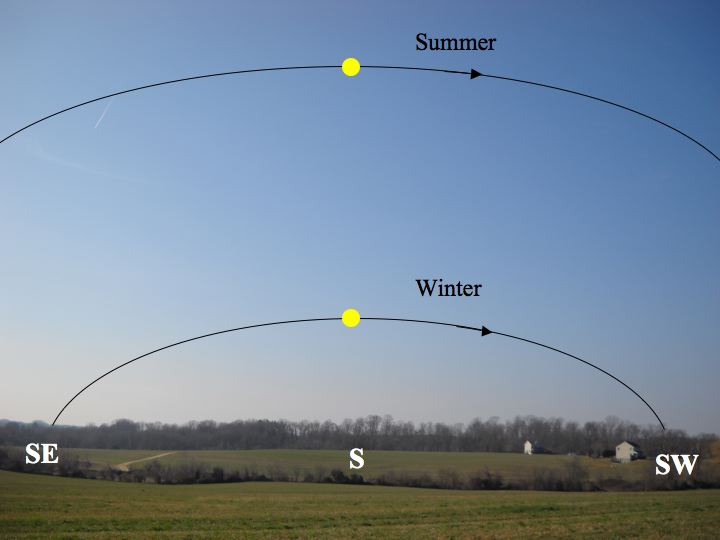
The Sun's track across the sky is much shorter and lower in the winter than in the summer. During the early fall, as the Sun moves lower in the southern sky, sunrises get later, and sunsets earlier.

So we are used to the fact that the length of daylight is significantly longer in summer than winter, and most of us know that the "longest day" (that is, the day when the Sun is above the horizon the longest) is the summer solstice, around June 21, when the Sun has reached its most northerly and longest track in our sky; and the "shortest day" is the winter solstice, around December 21, when the Sun has reached its most southerly and shortest track in our sky.

It would make sense, then, for the summer solstice to also be the date at which sunrise is earliest and sunset is latest; and for the winter solstice to be the date when sunrise is latest and sunset is earliest. However, that is not what happens! Nature sometimes defies our expectations.

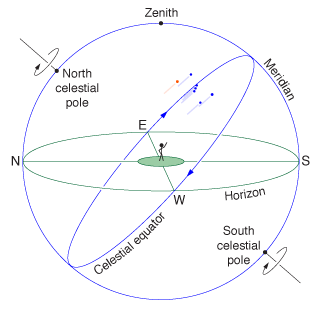
The local meridian is a great circle passing through the celestial poles and through the zenith of an observer's location on the planet. Image Credit: Daniel V. Schroeder

And that is because we have not talked about one other factor in sunrise and sunset times that is not at all obvious. It is that the Sun moves across the sky, in its apparent daily track, at slightly different rates at different parts of the year. Most of the Sun's east-to-west apparent motion in the sky is caused, of course, by the rotation of the Earth, which is quite uniform (to milliseconds per day). But a small part of the Sun's apparent daily motion depends on the position of the Earth in its orbit around the Sun. This component of the Sun's apparent motion varies by a small amount over the course of a year due to the elliptical shape of the Earth's orbit and to the tilt of the Earth's axis. The details of this variation are explained in detail elsewhere, but the overall effect is that the Sun's total apparent angular rate as it moves across the sky varies by as much as 0.07% from one part of the year to another. That doesn't seem like much, but it means that the length of the solar day, measured by successive transits of the Sun across the local meridian (successive noons on a sundial), can be as much as a half minute different from 24 hours, one way or the other.

Therefore, we effectively have two kinds of time. Time kept by the Sun's motion in the sky (apparent solar time) is not a uniform kind of time, like that kept by our clocks. Mechanical or electrical clocks run at a uniform rate, and that rate has been set to correspond to the average rate of the Sun across the sky over the course of the year. So our clock time (neglecting, of course, daylight time shifts) is a form of what is called mean solar time. Every day by our clocks has 24 hours exactly, but each day of apparent solar time can be different from 24 hours by as much as a half minute. At some parts of the year, the two kinds of time can accumulate a difference of as much as 16 minutes, which is one reason why sundials hardly ever seem to be correct. We are comparing apples and oranges: Sun time is not clock time.

Sundials hardly ever give the same time as our clocks. Sun time (technically, apparent solar time) is not the same as clock time (a type of mean solar time). The difference affects not only the time kept by sundials, but also the clock times of sunrise and sunset. Near both the winter and summer solstices, the changing difference between the two kinds of time has more effect on the times of sunrise and sunset than the slowly changing geometry of the Sun's track in the sky.

The two effects on sunrise and sunset time might be called, succinctly, the "geometric effect", which is the variation in the length of the Sun's track across the sky as a function of the season; and the "clock effect", caused by the fact that the Sun keeps its own time, which on any given day may be somewhat different from what our clocks say. Notice that the geometric effect tends to work oppositely on sunrise and sunset times; for example, in the fall, when the length of the Sun's track in the sky is getting shorter, sunrises get later and sunsets earlier. On the other hand, the clock effect works the same way on all Sun phenomena—if the Sun is "late" on a particular day (compared to the day before), then sunrise, sun transit (sundial noon), and sunset will all be "late" by the same amount. The technical name for the clock effect is the Equation of Time.

During the early fall, the geometric effect dominates the change in rise and set times; from one day to the next, the Sun is shifting ever more southward in the sky, and at mid northern latitudes, the total length of daylight (sunset time minus sunrise time) gets shorter by several minutes every day (see the Duration of Daylight/Darkness Table for One Year). For example, on October 15 at 40° north latitude, the Sun is above the horizon for 2½ fewer minutes than on the previous day. Based on that effect alone, we would expect sunrise to be later, and sunset earlier, by 1¼ minutes compared to the day before. The clock effect at this time of year is a rather minor factor; considering the clock effect alone (which is the same for all latitudes), the Sun is ¼ minute earlier in all of its phenomena on October 15 than it was on October 14. So the geometric effect dominates at this time of year in determining the times of rise and set.

As the fall progresses, though, several things change. For one thing, as we get into November, the geometric effect becomes less of a factor in the day-to-day changes. The Sun's southerly migration in the sky slows considerably as we get into December. (It comes to a stop at the winter solstice, around December 21, after which the Sun begins its slow march northward.) Also, around November 3, the clock effect changes sign and the Sun begins to run later and later each day. In fact, as the magnitude of the geometric effect is ramping down, the magnitude of the clock effect is ramping up. On December 15, the Sun is above the horizon for only ½ minute less than on the previous day, so sunrise will be later, and sunset earlier, by only ¼ minute compared to December 14, based on the geometric effect alone. But the clock effect shifts all Sun phenomena about ½ minute later by our clocks on December 15 than on December 14. So, adding the two effects together, the times of both sunrise and sunset on December 15 are later than on December 14. Evidently, we have already passed the date of earliest sunset, and the solstice has not yet occurred. The date of earliest sunset, about December 8 at a latitude of 40° north, is the date when the clock effect takes over from the geometric effect in having the greater influence on the times of sunset.

The date of latest sunrise is determined by similar considerations. As we have seen, in late December, both sunrise and sunset occur later each day. But after the solstice, the geometric effect, considered alone, tends to shift sunrise earlier as the Sun's daily track in the sky becomes more northerly and longer. But that effect is weaker than the clock effect—at least, for a while. Eventually, the geometric effect overcomes the clock effect's tendency to move all Sun phenomena later each day. The date of latest sunrise is therefore the date, after the solstice, when the geometric effect equals the clock effect in magnitude. That date is about January 5 at a latitude of 40° north. After that, the geometric effect takes over and the times of sunrise move consistently earlier.

Therefore, between the dates of earliest sunset and latest sunrise, the clock effect dominates the geometric effect in determining the times of sunrise and sunset for a given latitude.

The reason the dates of earliest sunset and latest sunrise depend on latitude is that the geometric effect is a greater factor at high latitudes. There, the length of the Sun's track across the sky varies more throughout the year. The clock effect is the same for all latitudes. So at higher latitudes, the dates of earliest sunset and latest sunrise are closer to the solstice; i.e., closer to when we expect them to be, based on the geometry of the Sun's seasonal motion. At the equator, there is no geometric effect at all—the Sun's daily track above the horizon is always exactly half a circle. The clock effect completely determines when sunrise and sunset occur there. Earliest sunset occurs around November 2 and latest sunrise occurs around February 11. But the total variation in sunrise or sunset times at the equator, over the year, amounts to only about a half hour.

Returning to the middle northern latitudes, sunrise and sunset times near the summer solstice are influenced by the geometric and clock effects in the same way as those near the winter solstice. However, the magnitude of the clock effect is not as large in June as in December. The date of earliest sunrise occurs before the solstice and the date of latest sunset occurs after.

Getting Technical . . .

The geometric effect mentioned above is a function of the Sun's declination, the term that astronomers use for the angle that the center of the Sun makes with the plane of the Earth's equator, as viewed by a fictitious observer at the center of the Earth. As the Earth orbits the Sun, the Sun's declination goes from +23.4° at the summer solstice to −23.4° at the winter solstice, and back again, passing through declination zero (that is, through the equatorial plane) at the two equinoxes. On the surface of the Earth, the length of time that the center of the Sun is above the horizon at any given latitude, in hours, is given approximately by

t_s = 2/15 arccos (–tan φ tan δ)

where φ is the latitude and δ is the Sun's declination. It is assumed that the value of the arccos function is given in degrees. This formula works only for latitudes between the arctic and antarctic circles. The time t_s changes over the course of a year as the Sun's declination δ changes. This simple formula neglects (1) atmospheric refraction at the horizon, (2) the small variation in the Sun's apparent rate of east-west motion across the sky due to the "clock effect", and (3) the small changes in the Sun's declination that occur during most days. In particular, it's worth noting here that sunrise and sunset are defined to occur when the top of the Sun (its upper limb) appears to be on the horizon, with atmospheric refraction taken into account, so the time between sunrise and sunset is always greater than t_s by at least a few minutes.

As mentioned above, astronomers call the clock effect the Equation of Time, which is the difference between apparent solar time and mean solar time. Civil time—what our clocks read—is a form of mean solar time on the local time zone's defining meridian (each time zone is based on a meridian with a longitude evenly divisible by 15°). Officially, civil time is an integral number of hours offset from Coordinated Universal Time, abbreviated UTC. The hour offset depends on the time zone and whether daylight time is in effect. UTC is the successor to Greenwich Mean Time and is synchronized worldwide to very high precision.

The dates of earliest sunset and latest sunrise are the dates before and after the winter solstice when, at a given latitude, the magnitude of half the daily change in t_s equals the magnitude of the daily change of the Equation of Time. Half the daily change in t_s is used because the geometric (or declination) effect is divided equally between sunrise and sunset. On the other hand, the change in the Equation of Time shifts the timing of all Sun phenomena by its full amount.

Approximate formulas for the Sun's declination and the Equation of Time are given on our page about computing Approximate Solar Coordinates. A table listing both the Sun's declination and the Equation of Time, for each day of the year, is printed in the annual booklet Astronomical Phenomena. The values in the table change from year to year but not by much. You can get the same information online, for a range of specific dates, here (be sure to select Apparent Geocentric Right Ascension and Declination for the Sun). If you use this data to make a graph of the Sun's declination as the y-axis and the Equation of Time as the x-axis, you obtain a figure-8 curve for the year called the analemma . The analemma is the pattern of Sun images that you would obtain if, using a fixed camera and a multiple exposure setting, you recorded the Sun at noon clock time on every day of the year that it was clear; see, for example this picture .